4.1 Spiroid
The word 'spiroid' has been adopted in this work because it seldom appears in everyday use of language; indeed it is absent from many dictionaries[n4.1] and the Google Ngram Viewer can be used to see how the word has been used relatively little in published works of the past two centuries.[n4.2] Any reference within this work to the (or a) spiroid will thus pertain specifically to my own conception of frequency-space representation.
[n4.1] No results are found via http://www.oxfordreference.com/search?q=spiroid whereas via http://www.thefreedictionary.com/spiroid definitions are found from various publications including Collins English Dictionary and Dorland's Medical Dictionary. (Last checked 20130309)
[n4.2] Compare http://books.google.com/ngrams/graph?content=spiroid%2CSpiroid&year_start=1800&year_end=2012 to the graph produced by adding, to the comma-separated search box, any one of these: toroid, sinusoid, cardioid, helicoid. In each case the graphed plots representing 'spiroid' and 'Spiroid' are reduced almost to flat by the adjusted scaling of the graph. (Last checked 20130312)
The spiroid can be viewed in the context of similar the models and diagrams that are found in numerous sources (cited variously below), but to introduce it as derivative of those would misrepresent its origins within my practice. So that the reader may observe the autogenous process through which the spiroid concept was founded, an abbreviated account of that incremental progression – extended along the way by additional a posteriori contextualisation of the concepts involved – is presented below. Central to this study is the idea of geometrical representations in compositional process; while in my own practice this came first as intuited drawing on paper, the cited contextualisation has both supported and fed into my understandings.
4.1.1 Circularity
The first of my sketches that would lead incrementally to the spiroid concept, was a visualisation of a six note scale with the pitch-classes of its notes being arranged, stepwise, on the circumference of a circle. That original drawing – which is reproduced below as Figure 4.1 – was used to contemplate all possible binary pitch pairings within the scale.
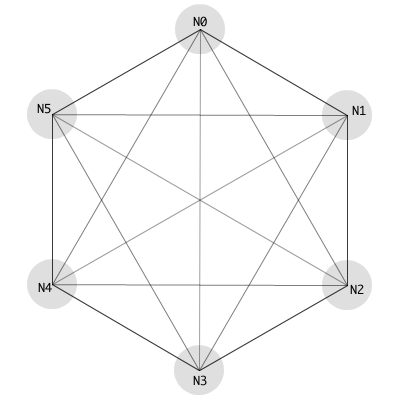
Figure 4.1: Showing six pitch-classes
The six pitch-classes that are labelled N0 to N5 in Figure 4.1 are of unspecified value in terms of their fundamental frequencies or intervalic ratios within this construct. The equidistant spacing within the sketch was not drawn to correspond to equal divisions of the octave, but rather as a purely abstract representation meant to imply equal potential of all constituent notes in the scale. Other than that significant distinction, however, this type of circular pitch-class-space is similar to the 'Tone Clock' diagrams described by Peter Schat (1993).
Composing within the twelve-tone tradition of the mid-to-late-twentieth-century, Peter Schat developed/discovered a system of 'chromatic tonality' as a tool to be utilised by composers (Schat, 2002). The term 'Tone Clock' was first used by Schat to refer to a 'Zodiac of the Twelve Tonalities' (Schat, 1993, p. 73, p. 81) in which 'twelve small clock-faces are contained within a larger clock-face' (see Figure 4.2) (McLeod, 1994, p. 113).
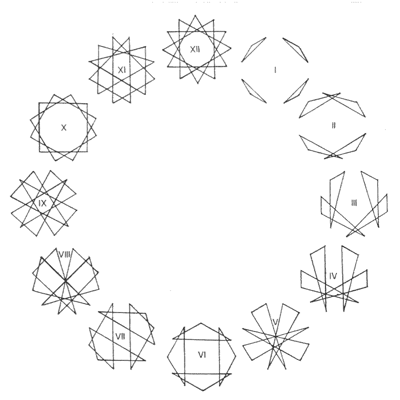
Figure 4.2: tone clock hours
We may refer to the singular clock-face, with its arrangement of the twelve tone equal temperament (12TET) pitch-classes on the circumference of a circle, as a 'tone-clock'. The space inside the tone-clock circle is used to draw lines that indicate relationships between the pitch-classes with disregard to the octave-level attribute; it was because of this visual similarity to the six-pitch-class diagram (Figure 4.1) that I took interest in The Tone Clock book.
Drawing triangles within tone-clock figures, Schat describes an exploration – 'in (tonal) space' – of tonality, where tonality is seen as arising from the triad: 'The triad is a (tone-)spatial creation' and there are 'no more than twelve different triads [that] can be formed' within the twelve tone system (Schat, 1993, p. 57).
All other triads conceivable can be reduced to these twelve basic forms. Therefore one can call these the 'Twelve Tonalities'. […] These triads fit four times into the module of the octave, in such a way that all twelve notes are always involved. (The Tenth Tonality is an exception […]) [The] descriptions of the different Hours (or Tonalities) is partly exact and partly subjective. Art is no science – there is nothing to prove. (Schat, 1993, p. 57–58)
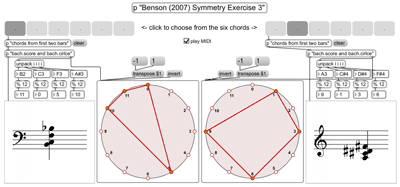
The tone-clock type construct is also recommended by David Benson in Music: A Mathematical Offering (2007) when an exercise on the subject of symmetry in music is set for the reader: Benson writes that – within the excerpt given as common music notation (CMN) – the 'symmetry in the first two bars of Schoenberg's Klavierstü?ck Op. 33a is somewhat harder to see' in comparison to previously given examples; Benson suggests that one 'may find it helpful to draw the chords on a circle' and illustrates the how the first chord of the passage would come out on a tone-clock circle (Benson, 2007, p. 320). To explore this exercise in software with interactive representations on screen, I made a patch[n4.3] in MaxMSP using newly available objects from the bach: automated composer's helper library (Agostini & Ghisi, 2012).[n4.4] Two of the GUI type objects from that library are employed in the maxpat: the bach.score object for displaying the CMN of the selected chords – selected via tabs of the tab objects in the patch – and the bach.circle object which brings a tone-clock type visual representation to the Max environment.[n4.5] Figure 4.3 shows the patch with the shapes of the first two chords displayed. A graphical clipping of the relevant text and illustrations from Benson are included in a sub-patch, and there is a basic 'play MIDI' option available.
[n4.3] BensonSymmetryEx3.maxpat which is in the BensonSymmetryEx3 folder in the chapter4 directory of the portfolio.
[n4.4] The maxpat was made using bach… library 'v0.6.7 alpha' which is copyrighted 2010 by Andrea Agostini and Daniele Ghisi; the latest version and further information can be found online via http://www.bachproject.net/
[n4.5] Although this object defaults to 'modulo twelve', any positive integer value can be used to set the number of points that appear around the circle, and although it is intended for representation of pitch-classes it could be used to other ends…
To add an observation of my own to this exercise, I suggest that if the tone-clock representation were to have at the twelve o'clock position aligned to mid-way between zero and one, rather than at zero, then the visual manifestation of the symmetries that are to be found here would be much more clearly shown. In other words, I would like to rotate, anti-clockwise by 15 degrees, the tone-clock representations that are on screen, but the bach.circle objects do not offer this adjustment parameter.
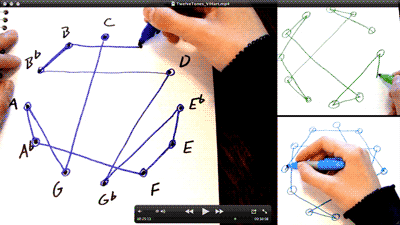
Further reference to Schoenberg can be found in a contemporary reflection on twelve-tone music that is provided by Vi Hart whose video on the subject (see Figure 4.4)is available both on YouTube (Hart, 2013a) and as a bit-torrent (Hart, 2013b).
4.1.2 Radially extending
The second step, the second sketch, in this simplified version of events describing the how the spiroid emerged in my work, was to extend the abstract pitch-class-space of Figure 4.1 to represent the discrete notes of that scale over multiple octaves, rather than just the pitch-classes. Figure 4.5 shows the initial, naïve, rendition of this radially extending step: by keeping the attribute of pitch-class aligned to that of visual angle on the plane, the octave-level attribute is readily manifest as proportional to the radius attribute on the plane. At this stage the representation is still highly abstracted from physical reality: although similar to the tone-clock representations described above, the equidistant spacing of its six pitch-classes unrelated to their distribution in 'tonal space'.
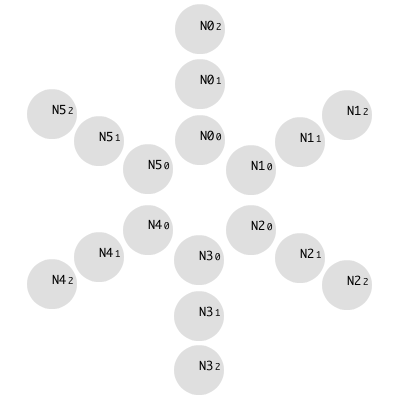
Figure 4.5: Three octaves of six pitch-classes (simple)
The visual rendering of three octaves that is seen in Figure 4.5 fails to represent the way that the N5 pitch of each octave is actually adjacent to the N0 pitch of the octave above. If one were to draw a line to go through each consecutive note of the scale as it is represented in Figure 4.5, then the spiral formed would be somewhat irregular: the visual distance representing the final interval of each octave turn is larger than the preceding intervals, causing a sudden change of angle in the spiral line that passes through them all.
To remedy that discrepancy, and thereby complete the specification of the spiroid archetype, the third step introduces two key elements: (1) the first of these is a conceptual shift, away from the purely abstract representation of pitch-classes from some particular scale, toward the more concrete and mathematical representation of a continuous frequency-space based on the pitch-class-circle of the tone-clock, as is the base of the Drobisch type helix described by Shepard (§2.2.2); and (2) second is the adoption of the Archimedean spiral equation as the mathematical basis of that representation.
4.1.3 On Spirals
The curve that was studied by Archimedes in his treatise On Spirals is 'the locus of a point which moves away from a fixed point with constant speed along a line which rotates with constant velocity' (Wells, 1991, p. 8). The polar equation of the Archimedean spiral has been discussed for its use in my conceptual model of a gramophone (§3.4.2). The constant rate of growth in the Archimedean spiral provides a good visual analogy to the constant nature of human perception of pitch where intervalic ratios are heard as being the same no matter where in the frequency-domain they occur. Figure 4.6 shows a computer rendered sketch of the spiroid archetype that highlights the visual equality of octave interval representations.
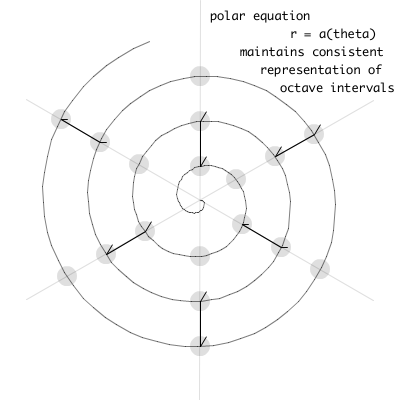
Figure 4.6: Sketch of the spiroid archetype
Each of the six radial lines in Figure 4.6 represents a specific pitch-class, and the fundamental frequency values corresponding to the notes of a scale are found where those radial lines intersect the spiral curve. Unlike the sketches that lead to this stage, recreated above as figures Figure 4.1 and Figure 4.5, what is shown in Figure 4.6 is now a spiroid type of representation wherein angular position is equated to a tone-clock type pitch-class-circle, and the equiangular distribution the six radii in Figure 4.6 thus correspond to what would be a whole-tone scale of 12TET. Unlike tone-clock representations, the spiroid-frequency-space is not limited to representation of quantised pitch-classes.
4.1.4 Curved continuum
The curve that is seen on a spiroid representation, such as in Figure 4.6, is a given as a visual manifestation of (a range of) the frequency-domain continuum. Only a limited range of that theoretically infinite continuum can ever be visually represented by the spiroid in any given manifestation, and that range limitation is determined primarily by the number of turns (number of octaves) that are to be drawn in the available screen space.[n4.6] The actual frequency range depicted is determined by both the number of octaves that are shown and an offset value for the starting frequency of the representation; the setting of these attributes being a matter of choice that will vary to suit different uses of the spiroid-frequency-space.
[n4.6] Software implementations are being assumed, though other manifestations of the spiroid are possible.
Frequency values on the spiroid are expressed natively as midi-pitch values, rather than Hertz, because the midi-pitch scale is more closely related to the human experience of the audible frequency-domain. It can be observed that to express an octave in terms of Hertz numeric value a 'doubling of frequency' is the language used; it is a relativistic relationship, and to say there is a change of x Hertz is almost meaningless without knowing what the value was to start with: a change of x may be perceived as an octave or as a quarter-tone where it is occurring. By contrast, it can be seen that there is permanent and stable relationship between human perception and numeric value in the midi-pitch scale; a 12TET quarter-tone is always a change of 0.5 in the midi-pitch scale, and an octave change is always expressed as a change in value by twelve. By extending above and below the 0–127 numerical range of the MIDI specification,[n4.7] and by allowing fractional values to exist between the integers, any required frequency value can be expressed as a midi-pitch value that can then manifest visually on the spiroid-frequency-space continuum curve.
[n4.7] The MIDI specification is described in (Roland Corporation U.S. & MIDI Manufacturers Association, 2009).
Pitch-class is manifest in the midi-pitch system as a modulo of twelve. Pitch-class is manifest on the spiroid continuum as angle with a modulo of 360 degrees. The 12TET semi-tone, is thus equivalent to 30 degrees of rotation on a spiroid-frequency-space representation. Values on the spiroid can therefore be converted between midi-pitch and angle, theta,[n4.8] by these equations:
[n4.8] Remember that theta is not bound to a single turn of the circle, but is rather the value that traverses the entire curve of the spiroid.
(midi pitch) = ( (theta) / 30 ) + (midi pitch offset)
(theta) = ( (midi pitch) - (midi pitch offset) ) · 30